
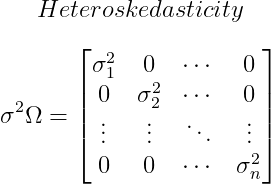

At least, one off-diagonal element is not equal to 0.
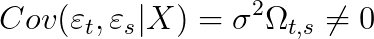

r -s는 Cov(t-s, t)임.
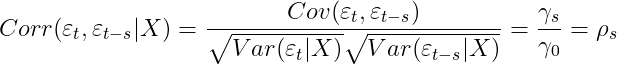
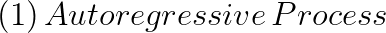
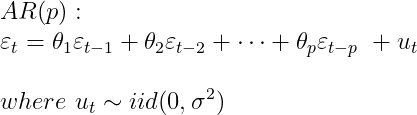
여기서 t기의 오차항은 과거의 오차항으로 설명되는 부분과 t기에 random하게 발생하는 백색잡음 u로 구성된다.
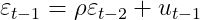
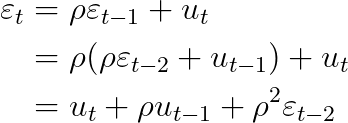
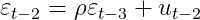
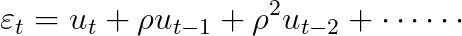
: Long memory
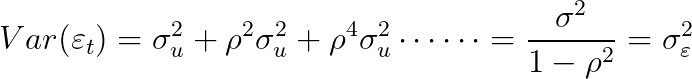
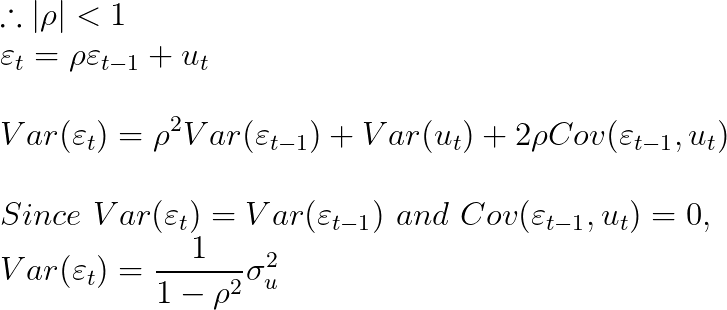
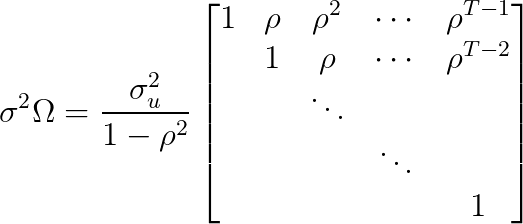
: Symmetric matrix
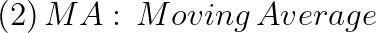
For simplicity, let's suppose X is independent of ε.
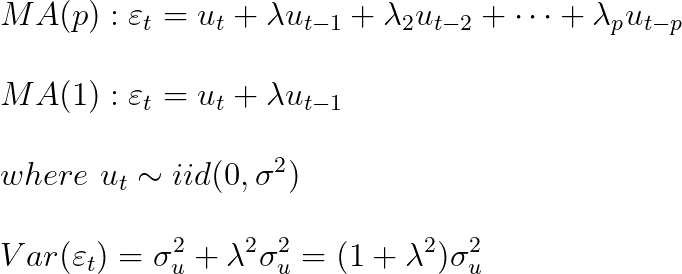
AR과는 달리 MA에서는 오차항이 과거의 오차항으로 설명되는 게 아니라 이전의 white noises에 의해 설명되고 있다.
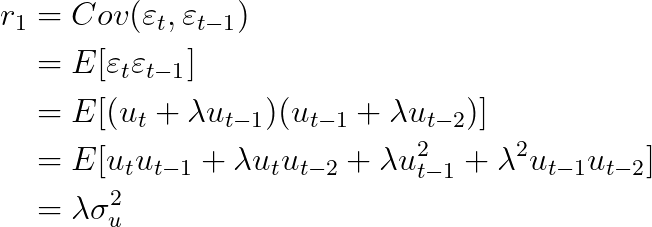
오차항은 zero mean을 가지므로, 오차항끼리 직교하면 선형관계가 존재하지 않는다.
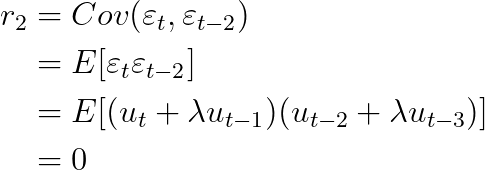

: Short memory
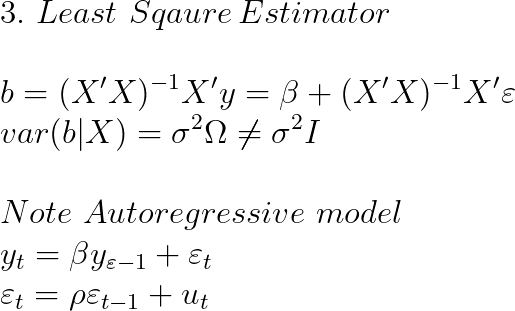
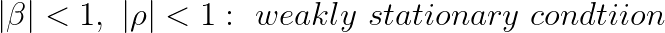

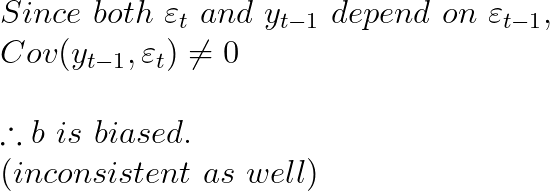
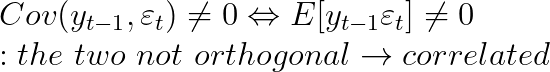
이분산의 경우와 마찬가지로 오차항에 자기상관(autocorrelation)이 있는 경우 OLS 추정량 b는 unbiased하고 consistent지만, efficient하지 못하여 분산의 추정량이 달라지고 결과적으로 이를 이용한 가설 검정이 틀리게 됨.
예외적으로 자기회귀 모형(autoregressive model)에 자기상관이 있을 경우엔 OLS 추정량 b에도 편의가 발생하고 inconsistent하게 된다.
Note:
OLS with hetero-, consistent estimator: White's hetero- consistent variance estimator
OLS with Newey-West HAC variance estimator
| Cross-Sectional Data | Time-Series Data |
| heteroskedasticity (O) autocorrelation (X) White's heteroskedasticity consistent variance estimator |
heteroskedasticity(△) autocorrelation(O) Newey-West HAC variance estimator |

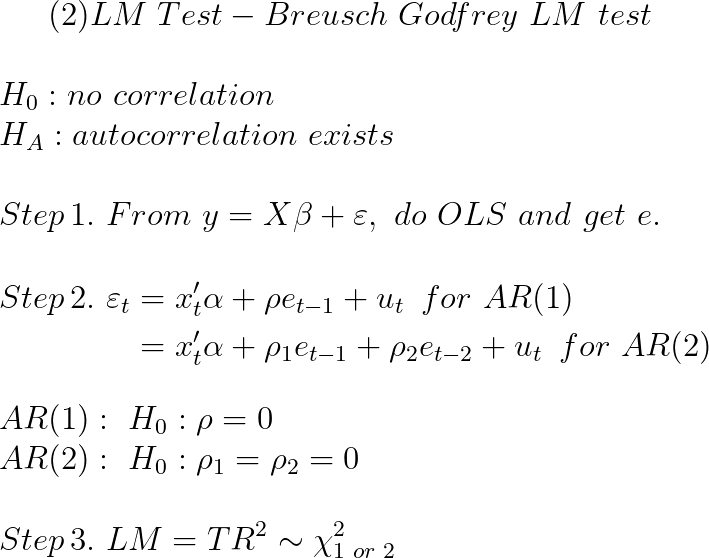
데이터의 개수가 T개 이고 제약이 p개일 때, TR^2은 제약 개수만큼의 자유도를 지닌 카이제곱 분포를 따른다.
여기서 결정계수 R^2은 step 2에서 구한 것이다.
'계량경제학' 카테고리의 다른 글
| 오차항의 표본분산의 일치성 증명 (0) | 2021.11.23 |
|---|---|
| 11월 20일 계량 (0) | 2021.11.20 |
| d (0) | 2021.11.19 |
| 11.16 -1 (0) | 2021.11.16 |
| Rank(X'X)=k, Full Rank (0) | 2021.10.13 |


